Instructions
In this homework, you are required to complete the problems described in section 3.
The starter code for these problems is provided in hw04.py, ADT.py and shakespeare.py.
We have also prepared two optional problems just for fun in section 3. You can find further descriptions there.
Submission: As instructed before, you need to submit your work with Ok by python ok --submit.
You may submit more than once before the deadline,
and your score of this assignment will be the highest one of all your submissions.
Readings: You might find the following references to the textbook useful:
Required Problems
In this section, you are required to complete the problems below and submit your code.
Remember, you can use ok to test your code:
$ python ok # test all functions
$ python ok -q <func> # test single function
Problem 1: Couple (100pts)
Implement the function couple, which takes in two lists and returns a list that contains lists with i-th elements of two sequences coupled together. You can assume the lengths of two sequences are the same. Try using a list comprehension.
def couple(lst1, lst2):
"""Return a list that contains lists with i-th elements of two sequences
coupled together.
>>> lst1 = [1, 2, 3]
>>> lst2 = [4, 5, 6]
>>> couple(lst1, lst2)
[[1, 4], [2, 5], [3, 6]]
>>> lst3 = ['c', 6]
>>> lst4 = ['s', '1']
>>> couple(lst3, lst4)
[['c', 's'], [6, '1']]
"""
assert len(lst1) == len(lst2)
"*** YOUR CODE HERE ***"
Problem 2: Mobiles (400pts)
Acknowledgements:
This mobile example is based on a classic problem from Structure and Interpretation of Computer Programs, Section 2.2.2.
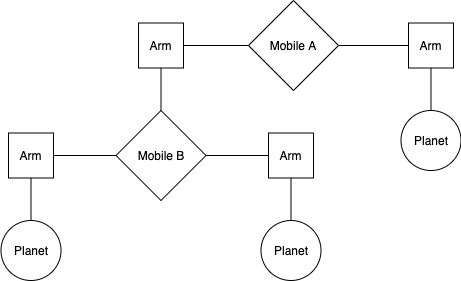
We are making a planetarium mobile. A mobile is a type of hanging sculpture. A binary mobile consists of two arms. Each arm is a rod of a certain length, from which hangs either a planet or another mobile.
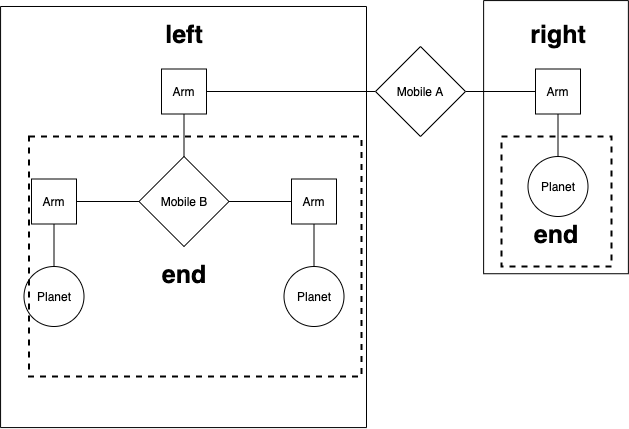
We will represent a binary mobile using the data abstractions below:
- A mobile has a left arm and a right arm.
- An arm has a positive length and something hanging at the end, either a mobile or planet.
- A planet has a positive size.
Problem 2.1 Weights (100pts)
Implement the planet data abstraction by completing the planet constructor and the size selector
so that a planet is represented using a two-element list where the first element is the string 'planet' and the second element is its size.
The total_weight example is provided to demonstrate use of the mobile, arm, and planet abstractions.
# The constructor and selectors of the planet
def planet(size):
"""Construct a planet of some size.
>>> planet(5)
['planet', 5]
"""
assert size > 0
"*** YOUR CODE HERE ***"
def size(w):
"""Select the size of a planet.
>>> p = planet(5)
>>> size(p)
5
"""
assert is_planet(w), 'must call size on a planet'
"*** YOUR CODE HERE ***"
def is_planet(w):
"""Whether w is a planet."""
return type(w) == list and len(w) == 2 and w[0] == 'planet'
# examples and usage
def examples():
t = mobile(arm(1, planet(2)),
arm(2, planet(1)))
u = mobile(arm(5, planet(1)),
arm(1, mobile(arm(2, planet(3)),
arm(3, planet(2)))))
v = mobile(arm(4, t), arm(2, u))
return (t, u, v)
def total_weight(m):
"""Return the total weight of m, a planet or mobile.
>>> t, u, v = examples()
>>> total_weight(t)
3
>>> total_weight(u)
6
>>> total_weight(v)
9
"""
"*** YOUR CODE HERE ***"
Note: the code listed above is the part you should fill in for the lab, see hw04.py for the complete code.
Problem 2.2: Balanced (100pts)
Implement the balanced function, which returns whether m is a balanced mobile.
A mobile is balanced if two conditions are both met:
- The torque applied by its left arm is equal to that applied by its right arm. Torque of the left arm is the length of the left rod multiplied by the total weight hanging from that rod. Likewise for the right.
- Each of the mobiles hanging at the end of its arms is balanced.
Planets themselves are balanced.
def balanced(m):
"""Return whether m is balanced.
>>> t, u, v = examples()
>>> balanced(t)
True
>>> balanced(v)
True
>>> w = mobile(arm(3, t), arm(2, u))
>>> balanced(w)
False
>>> balanced(mobile(arm(1, v), arm(1, w)))
False
>>> balanced(mobile(arm(1, w), arm(1, v)))
False
"""
assert is_mobile(m)
"*** YOUR CODE HERE ***"
Problem 2.3: Mobile to Tree (200pts)
Implement totals_tree, which takes a mobile (or planet) and returns a tree whose root is the total weight of the input.
For a planet, the result should be a leaf.
For a mobile, the result should be a tree and its branches should be
the totals_tree for each ends of the arms.
from ADT import tree, label, branches, is_leaf, print_tree
def totals_tree(m):
"""Return a tree representing the mobile/planet with its total weight at the root.
>>> t, u, v = examples()
>>> print_tree(totals_tree(t))
3
2
1
>>> print_tree(totals_tree(u))
6
1
5
3
2
>>> print_tree(totals_tree(v))
9
3
2
1
6
1
5
3
2
"""
assert is_mobile(m) or is_planet(m)
"*** YOUR CODE HERE ***"
Hint: you may want to use some helper functions imported from ADT.py.
Problem 3: Trees (600pts)
Recall that the tree abstract data types mentioned in class, can be recursively defined using a root node and (sub)trees.
Tree ADT has one constructor:
tree(label, branches=[]): Creates a tree with the given label and branches.
We also have the following default selectors in order to get the information for each tree:
label(tree): returns thetree's label.branches(tree): returns thetree's branches.is_leaf(object): returns the if atreeis a leaf.
Problem 3.1: Add trees (200pts)
Define the function add_trees, which takes in two trees and returns a new tree where each corresponding node from the first tree is added with the node from the second tree. If a node at any particular position is present in one tree but not the other, it should be present in the new tree as well.
Hint:
label(t)may not be a number.- returns a new tree means that you should call the
treeconstructor for every nodes of the returned tree.- Do not modify the given trees or reuse branches directly from the given trees, call
treeconstructors instead.- Do not simply call
list(branches(t))to copy the branches of a treet, as it creates a shallow-copy instead of a deep-copy of the list.- You may want to use
copy_treedefined inADT.pyto deep-copy a tree.
def add_trees(t1, t2):
"""
>>> numbers = tree(1,
... [tree(2,
... [tree(3),
... tree(4)]),
... tree(5,
... [tree(6,
... [tree(7)]),
... tree(8)])])
>>> print_tree(add_trees(numbers, numbers))
2
4
6
8
10
12
14
16
>>> print_tree(add_trees(tree(2), tree(3, [tree(4), tree(5)])))
5
4
5
>>> print_tree(add_trees(tree(2, [tree(3)]), tree(2, [tree(3), tree(4)])))
4
6
4
>>> print_tree(add_trees(tree(2, [tree(3, [tree(4), tree(5)])]), \
tree(2, [tree(3, [tree(4)]), tree(5)])))
4
6
8
5
5
"""
"*** YOUR CODE HERE ***"
Problem 3.2: Big Path (100pts)
A path through a tree is a list of adjacent node values that starts with the root value. Paths can end at any node but they must always go from one node to one of its branches and may not go upwards.
For example, the paths of tree(1, [tree(2), tree(3, [tree(4), tree(5)])]) are
[1]
[1, 2]
[1, 3]
[1, 3, 4]
[1, 3, 5]
Implement bigpath, which takes a tree t and an integer n. It returns the number of paths in t whose sum is at least n. Assume that all node values of t are integers.
def bigpath(t, n):
"""Return the number of paths in t that have a sum larger or equal to n.
>>> t = tree(1, [tree(2), tree(3, [tree(4), tree(5)])])
>>> bigpath(t, 3)
4
>>> bigpath(t, 6)
2
>>> bigpath(t, 9)
1
"""
"*** YOUR CODE HERE ***"
Problem 3.3: Bigger Path (100pts)
Now, implement bigger_path, which removes the restriction that paths must begin at the root -- they can begin at any node. You can use bigpath to help your implementation.
def bigger_path(t, n):
"""Return the number of paths in t that have a sum larger or equal to n.
>>> t = tree(1, [tree(2), tree(3, [tree(4), tree(5)])])
>>> bigger_path(t, 3)
9
>>> bigger_path(t, 6)
4
>>> bigger_path(t, 9)
1
"""
"*** YOUR CODE HERE ***"
Problem 3.4: Trie (200pts)
Write a function has_path that takes in a tree t and a string word.
It returns True if there is a path starting from the root,
along which the entries spell out the word. Otherwise, it returns False.
(This data structure is called a trie, and it has a lot of cool applications!---think autocomplete).
You may assume that every node's label is exactly one character.
def has_path(t, word):
"""Return whether there is a path in a tree where the entries along the path
spell out a particular word.
>>> greetings = tree('h', [tree('i'),
... tree('e', [tree('l', [tree('l', [tree('o')])]),
... tree('y')])])
>>> print_tree(greetings)
h
i
e
l
l
o
y
>>> has_path(greetings, 'h')
True
>>> has_path(greetings, 'i')
False
>>> has_path(greetings, 'hi')
True
>>> has_path(greetings, 'hello')
True
>>> has_path(greetings, 'hey')
True
>>> has_path(greetings, 'bye')
False
"""
assert len(word) > 0, 'no path for empty word.'
"*** YOUR CODE HERE ***"
Mock Exam Problems
In this section, you can take a mock exam to check your understanding about trees and lists.
Download the mock exam here and print it out.
说明:
- 你应该先完成本周的作业,有空余时间再来做mock exam。
- 文件中是2022级其中考试的部分习题,建议你打印出来,限时(50min)完成。
- 作为提醒,期中和期末只占25%的总评成绩,所以会有部分很难的题目;即使你没有做出来,依然可以拿到比较满意的分数。
Just for fun Problems
This section is out of scope for our course, so the problems below is optional. That is, the problems in this section don't count for your final score and don't have any deadline. Do it at any time if you want an extra challenge.
At this time, we don't provide Online Judgement. The local doctest is enough for you to check your answer. You can find the starter code in shakespeare.py.
Problem 4: Fold Tree (0pts)
Use
python ok -q treeto test your implementation.
It is often the case that we want to fold a tree into a value. Consider the following implementations of count_leaves and label_sum.
def count_leaves(t):
"""Count the leaves of a tree."""
if is_leaf(t):
return 1
result = 0
for b in branches(t):
result += count_leaves(b)
return result
def label_sum(t):
"""Sum up the labels of all nodes in a tree."""
if is_leaf(t):
return label(t)
result = label(t)
for b in branches(t):
result += label_sum(b)
return result
or, by clever usage of function sum and list comprehension, we can equivalently write
def count_leaves(t):
"""Count the leaves of a tree."""
if is_leaf(t):
return 1
return sum([count_leaves(b) for b in branches(t)])
def label_sum(t):
"""Sum up the labels of all nodes in a tree."""
if is_leaf(t):
return label(t)
return label(t) + sum([label_sum(b) for b in branches(t)])
You may find these implementations look quite similar, as they both:
- return something immediately at a base case when
tis a leaf - recursively apply the function to branches, and sum up the results of the branches
To capture this insight, we can define a function fold_tree which takes in a function base_func and a function merge_func.
You can feel free to define the meaning and usage of base_func and merge_func.
Then use fold_tree to implement count_leaves, label_sum and preorder.
def fold_tree(t, base_func, merge_func):
"""Fold tree into a value according to base_func and merge_func"""
"*** YOUR CODE HERE ***"
def count_leaves(t):
"""Count the leaves of a tree.
>>> t = tree(1, [tree(2), tree(3, [tree(4), tree(5)])])
>>> count_leaves(t)
3
"""
return fold_tree(t, 'YOUR EXPRESSION HERE', 'YOUR EXPRESSION HERE')
def label_sum(t):
"""Sum up the labels of all nodes in a tree.
>>> t = tree(1, [tree(2), tree(3, [tree(4), tree(5)])])
>>> label_sum(t)
15
"""
return fold_tree(t, 'YOUR EXPRESSION HERE', 'YOUR EXPRESSION HERE')
def preorder(t):
"""Return a list of the entries in this tree in the order that they
would be visited by a preorder traversal.
>>> t = tree(1, [tree(2), tree(3, [tree(4), tree(5)])])
>>> preorder(t)
[1, 2, 3, 4, 5]
"""
return fold_tree(t, 'YOUR EXPRESSION HERE', 'YOUR EXPRESSION HERE')
Since functions are values in Python, we can also use fold_tree to fold a tree to a function.
We can simply use fold_tree and curring to define a function has_int which checks if a given integer is contained in a tree:
def has_int(tree, i): # Without fold_tree
"""Return if an integer is contained in a tree
>>> has_int(tree(1, [tree(2, tree(3)), tree(4)]), 1)
True
>>> has_int(tree(1, [tree(2, tree(3)), tree(4)]), 5)
False
"""
return label(tree) == i or any([has_int(b) for b in branches(tree)])
def has_int(tree, i): # With fold_tree
"""Return if an integer is contained in a tree
>>> has_int(tree(1, [tree(2, [tree(3)]), tree(4)]), 1)
True
>>> has_int(tree(1, [tree(2, [tree(3)]), tree(4)]), 5)
False
"""
def base_func(l):
return lambda i: l == i
def merge_func(l, bs):
return lambda i: l == i or any([b(i) for b in bs])
return fold_tree(tree, base_func, merge_func)(i)
Note: If you don't know
any, try "help(any)" in python interactive shell or searches the documentation.
Now, use the same technique to define has_path:
def has_path_fold(t, word):
"""Return whether there is a path in a tree where the entries along the path
spell out a particular word.
>>> greetings = tree('h', [tree('i'),
... tree('e', [tree('l', [tree('l', [tree('o')])]),
... tree('y')])])
>>> print_tree(greetings)
h
i
e
l
l
o
y
>>> has_path_fold(greetings, 'h')
True
>>> has_path_fold(greetings, 'i')
False
>>> has_path_fold(greetings, 'hi')
True
>>> has_path_fold(greetings, 'hello')
True
>>> has_path_fold(greetings, 'hey')
True
>>> has_path_fold(greetings, 'bye')
False
"""
assert len(word) > 0, 'no path for empty word.'
return fold_tree(t, 'YOUR EXPRESSION HERE', 'YOUR EXPRESSION HERE')
Problem 5: Shakespeare and Dictionaries (0pts)
Note that this problem is in
shakespeare.py, nothw04.py. It will not be tested and graded by OJ.
We will use dictionaries to approximate the entire works of Shakespeare! We're going to use a bigram language model. Here's the idea: We start with some word -- we'll use "The" as an example. Then we look through all of the texts of Shakespeare and for every instance of "The" we record the word that follows "The" and add it to a list, known as the successors of "The". Now suppose we've done this for every word Shakespeare has used, ever.
Let's go back to "The". Now, we randomly choose a word from this list, say "cat". Then we look up the successors of "cat" and randomly choose a word from that list, and we continue this process. This eventually will terminate in a period (".") and we will have generated a Shakespearean sentence!
The object that we'll be looking things up in is called a "successor table", although really it's just a dictionary. The keys in this dictionary are words, and the values are lists of successors to those words.
Problem 5.1: Successor Tables
Here's an incomplete definition of the build_successors_table function. The input is a list of words (corresponding to a Shakespearean text), and the output is a successors table. (By default, the first word is a successor to "."). See the example below.
def build_successors_table(tokens):
"""Return a dictionary: keys are words; values are lists of successors.
>>> text = ['We', 'came', 'to', 'investigate', ',', 'catch', 'bad', 'guys', 'and', 'to', 'eat', 'pie', '.']
>>> table = build_successors_table(text)
>>> sorted(table)
[',', '.', 'We', 'and', 'bad', 'came', 'catch', 'eat', 'guys', 'investigate', 'pie', 'to']
>>> table['to']
['investigate', 'eat']
>>> table['pie']
['.']
>>> table['.']
['We']
"""
table = {}
prev = '.'
for word in tokens:
if prev not in table:
"*** YOUR CODE HERE ***"
"*** YOUR CODE HERE ***"
prev = word
return table
Problem 5.2: Construct the Sentence
Let's generate some sentences! Suppose we're given a starting word. We can look up this word in our table to find its list of successors, and then randomly select a word from this list to be the next word in the sentence. Then we just repeat until we reach some ending punctuation.
This might not be a bad time to play around with adding strings together as well. Let's fill in the construct_sent function!
def construct_sent(word, table):
"""Prints a random sentence starting with word, sampling from
table.
>>> table = {'Wow': ['!'], 'Sentences': ['are'], 'are': ['cool'], 'cool': ['.']}
>>> construct_sent('Wow', table)
'Wow!'
>>> construct_sent('Sentences', table)
'Sentences are cool.'
"""
import random
result = ''
while word not in ['.', '!', '?']:
"*** YOUR CODE HERE ***"
return result.strip() + word
Hint: to randomly select from a list, import the Python random library with
import randomand use the expressionrandom.choice(my_list).
Problem 5.3: Become Shakespeare
Great! Now let's try to run our functions with some actual data. The following snippet included in the skeleton code will return a list containing the words in all of the works of Shakespeare.
def shakespeare_tokens(url='https://www.composingprograms.com/shakespeare.txt'):
"""Return the words of Shakespeare's plays as a list."""
from urllib.request import urlopen
shakespeare = urlopen(url)
return shakespeare.read().decode(encoding='ascii').split()
Uncomment the following two lines to run the above function and build the successors table from those tokens.
# Uncomment the following two lines
# tokens = shakespeare_tokens()
# table = build_successors_table(tokens)
Next, let's define a utility function that constructs sentences from this successors table:
>>> def sent():
... return construct_sent('The', table)
>>> sent()
" The plebeians have done us must be news-cramm'd."
>>> sent()
" The ravish'd thee , with the mercy of beauty!"
>>> sent()
" The bird of Tunis , or two white and plucker down with better ; that's God's sake."
Notice that all the sentences start with the word "The". With a few modifications, we can make our sentences start with a random word. The following random_sent function (defined in your starter file) will do the trick:
def random_sent():
import random
return construct_sent(random.choice(table['.']), table)
Go ahead and load your file into Python (be sure to use the -i flag). You can now call the random_sent function to generate random Shakespearean sentences!
>>> random_sent()
" Long live by thy name , then , Dost thou more angel , good Master Deep-vow , And tak'st more ado but following her , my sight Of speaking false!"
>>> random_sent()
" Yes , why blame him , as is as I shall find a case , That plays at the public weal or the ghost."