1. Instructions
In this lab, you have three tasks:
- Think about what python would display if the code described in section 3 were input to a python interpreter, better without directly running python.
- Draw environment diagrams for the code in section 4.
- Complete the required problems described in section 5 and submit your code with Ok as instructed in lab00. The starter code for these problems is provided in
lab03.py, which is distributed as part of the lab materials in thecodedirectory.
Submission: As instructed before, you need to submit your work with Ok by python ok --submit.
You may submit more than once before the deadline,
and your score of this assignment will be the highest one of all your submissions.
Readings: You might find the following reference to the textbook useful:
2. Review
Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the next section and refer back here when you get stuck.
2.1 Recursion
A recursive function is a function that calls itself in its body, either directly or indirectly. Recursive functions have three important components:
- Base case(s), the simplest possible form of the problem you're trying to solve.
- Recursive case(s), where the function calls itself with a simpler argument as part of the computation.
- Combining results from recursive calls to solve the full problem.
Q: What does "simpler" mean?
A: Well, for integer
iandj,iis simpler thanjiffi < jQ: So, "simpler" means less than?
A: "Generalized" less than. This can be tricky for some problems, see Problem 1.
Let's look at the canonical example, factorial.
Factorial, denoted with the ! operator, is defined as: $$ n! = \prod_{i=1}^n i = n \times (n-1) \times \dots \times 1 $$ Or, equivalently, in a recursive way: $$ n! = \begin{cases} 1 & n=0 \\ n\times (n-1)! & \text{otherwise} \end{cases} $$ For example: $$ 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 $$
An iterative implementation for factorial might look like this:
def factorial(n):
result, i = 1, 1
while i <= n:
result = result * i
i += 1
return result
In contrast, a recursive implementation for factorial is as follows, note how it resembles the recursive definition of factorial:
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
- Base case: by the definition of factorial, the simplest possible form would be
0!sincen == 0is the smallest number we can compute the factorial of. - Recursive case: follows immediately from the definition of factorial, i.e.,
factorial(n) = n * factorial(n - 1), wherefactorial(n - 1)is a recursive call tofactorialwith a simpler argumentn - 1. - Combining results: as for factorial, simply multiply
factorial(n - 1)bynand return the result.
In this lab you will be implementing recursive functions to solve some problems. Here are some general tips:
- Paradoxically, to write a recursive function, you must assume that the function is fully functional before you finish writing it; this is called the recursive leap of faith.
- Consider how you can solve the current problem using the solution to a simpler version of the problem. The amount of work done in a recursive function can be deceptively little: remember to take the leap of faith and trust the recursion to solve the slightly smaller problem without worrying about how.
- Think about what the answer would be in the simplest possible case(s). These will be your base cases - the stopping points for your recursive calls. Make sure to consider the possibility that you're missing base cases (this is a common way recursive solutions fail).
- It may help to write an iterative version first.
2.2 Tree Recursion
A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.
A classic example of a tree recursion function is finding the nth Fibonacci number:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n - 1) + fib(n - 2)
Calling fib(6) results in the following call structure (where f is fib):
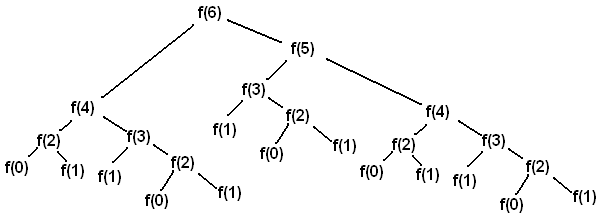
Each f(i) node represents a recursive call to fib with argument i. Each recursive call makes another two recursive calls. f(0) and f(1) do not make any recursive calls because they are the base cases of the function. Because of these base cases, we are able to terminate the recursion and beginning accumulating the values.
Generally, tree recursion is effective when you want to explore multiple possibilities or choices at a single step. In these types of problems, you make a recursive call for each choice or for a group of choices during each step, and finally combine those results to conclude an optimal choice. Here are some examples:
- Given a list of paid tasks and a limited amount of time, which tasks should you choose to maximize your pay? This is actually a variation of the Knapsack problem, which focuses on finding some optimal combination of different items.
- Suppose you are lost in a maze and see several different paths. How do you find your way out? This is an example of path finding, and is tree recursive because at every step, you could have multiple directions to choose from that could lead out of the maze.
- Your dryer costs $2 per cycle and accepts all types of coins. How many different combinations of coins can you create to run the dryer? This is similar to the partitions problem from the textbook.
3. What Would Python Display?
In this section, you need to think about what python would display if the code given were input to a python interpreter.
Question 1: Tricky Functions
Submit your answers with
python ok -q q1 -u.In What Would Python Display problems, always follow these rules:
For each of the expressions in the table below, write the output displayed by the interactive Python interpreter when the expression is valued. The output may have multiple lines or no lines.
- If an error occurs, write
Error, but include all output displayed before the error.- If an expression evaluates to a function value, write
Function.- If an expression would take forever to evaluate, write
Forever.- If the interpretor prints nothing, write
Nothing.
Secret: The following questions are inspired by the problems some of you met in lab02/hw02.
>>> def f(x):
... return x * x
>>> g = lambda x: f(x + 1)
>>> g
______
>>> g(1)
______
>>> print(g(2))
______
>>> f = lambda x: f(x + 1)
>>> f(1) # When is the return expression of a lambda expression executed?
______
>>> def f1(n):
... def f2(x):
... if x == 0:
... return 'cake'
... else:
... print('The cake is a lie.')
... n -= x
... return f2(n)
... return f2
>>> f1(2)
______
>>> f1(2)(2)
______
Question 2: Squared Virahanka Fibonacci
Submit your answers with
python ok -q q2 -u.
Background:
In the Squared Virahanka Fibonacci sequence, each number in the sequence is the square of the sum of the previous two numbers in the sequence. The first 0th and 1st number in the sequence are 0 and 1, respectively. The recursive virfib_sq function takes in an argument n and returns the nth number in the Square Virahanka Fibonacci sequence.
>>> def virfib_sq(n):
... print(n)
... if n <= 1:
... return n
... return (virfib_sq(n - 1) + virfib_sq(n - 2)) ** 2
>>> virfib_sq
______
>>> r0 = virfib_sq(0)
______
>>> virfib_sq(1)
______
>>> r1 = virfib_sq(1)
______
>>> r2 = virfib_sq(2)
______
>>> r3 = virfib_sq(3)
______
>>> r3
______
>>> (r1 + r2) ** 2
______
>>> r4 = virfib_sq(4)
______
>>> r4
______
4. Environment Diagrams
In this section, you need to draw an environment diagram for the code given.
You don't have to submit your answers. But similar problems will appear on the exam.
Question 3: In and Out
Draw the environment diagram of the following code:
x = 3
def out(g, m):
x = 5 * m
def inner():
return x
if m == 0:
return g
else:
return out(inner, m-1)
v = out(out, 1)()
After drawing the diagram, compare it to the correct one here.
Then predict what would python display and submit your answer with python ok -q q3 -u.
5. Required Problems
In this section, you are required to complete the problems below and submit your code with Ok as instructed in lab00 to get your answer scored.
Problem 1: F91 (100pts)
The f91 function is a recursive function, defined by the computer scientist John McCarthy as a test case for formal verification within computer science.
Write a recursive function f91 that takes a single argument n,
- returns
n - 10whenn > 100 - returns
f91(f91(n + 11))whenn ≤ 100
def f91(n):
"""Takes a number n and returns n - 10 when n > 100,
returns f91(f91(n + 11)) when n ≤ 100.
>>> f91(1)
91
>>> f91(2)
91
>>> f91(100)
91
"""
"*** YOUR CODE HERE ***"
Q: It seems that the argument of
f91's recursive calls is not always simpler in terms of less-than relation of integers.A: Oh, the meaning of "simpler" is not that simple ...
Problem 2: Monotone (100pts)
A number is said to have monotone digits if its digits have an non-decreasing order from left to right when written down.
For example, 1234 and 24555 have monotone digits, while 22000130 and 2024 don't.
Now, please write a recursive function is_monotone, which takes as input a number n and returns whether n has monotone digits.
Specifically, is_monotone returns True if n has monotone digits, and returns False if not.
def is_monotone(n):
"""Returns whether n has monotone digits.
Implement using recursion!
>>> is_monotone(22000130)
False
>>> is_monotone(1234)
True
>>> is_monotone(24555)
True
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(LAB_SOURCE_FILE, 'is_monotone', ['While', 'For'])
True
"""
"*** YOUR CODE HERE ***"
Problem 3: Climb Stairs (200pts)
Nolan lives on the sixth floor of the dormitory building and feels frustrated about climbing such a long flight of stairs every day. He is wondering how many different ways he can go up the stairs. He knows that going up the stairs requires n steps, where n is a positive integer, and he can either take 1 or 2 steps each time.
Please help him write a function count_stair_ways which takes in the total steps n and returns the number of ways to climb up a flight of n stairs.
def count_stair_ways(n):
"""Returns the number of ways to climb up a flight of
n stairs, moving either 1 step or 2 steps at a time.
>>> count_stair_ways(3)
3
>>> count_stair_ways(4)
5
>>> count_stair_ways(10)
89
"""
"*** YOUR CODE HERE ***"
Nolan realized that he could take more steps at a time! Now he is able to take up to and including k steps at a time, where k is a positive integer.
Write a function count_k that takes in the total steps n and maximum steps k at a time, then return the number of ways to climb up a flight of n stairs. (k may be larger than n)
Hint: Your solution will follow a very similar logic to what you did in
count_stair_ways.
def count_k(n, k):
"""Counts the number of paths to climb up a flight of n stairs,
taking up to and including k steps at a time.
>>> count_k(3, 3) # 3, 2 + 1, 1 + 2, 1 + 1 + 1
4
>>> count_k(4, 4)
8
>>> count_k(10, 3)
274
>>> count_k(300, 1) # Only one step at a time
1
>>> count_k(3, 5) # Take no more than 3 steps
4
"""
"*** YOUR CODE HERE ***"
Problem 4: Insect Combinatorics (200pts)
Consider an insect in an M by N grid. The insect starts at the bottom left corner, (0, 0), and wants to end up at the top right corner, (M-1, N-1). The insect is only capable of moving right or up by one step (e.g., from (0, 0) to (0, 1) or (1, 0)).
Write a function paths that takes a grid's length M and width N as input, then paths is supposed to return the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)
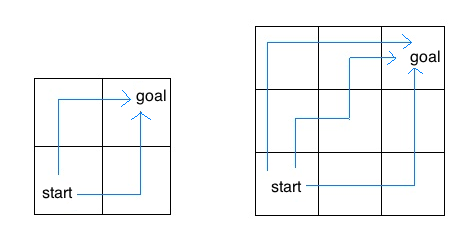
For example, a 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For a 3 by 3 grid, the insect has 6 different paths (only 3 are shown above).
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
Problem 5: Maximum Subsequence (200pts)
A subsequence of a number is a series of (not necessarily contiguous) digits of the number. For example, 12345 has subsequences that include 123, 234, 124, 245, etc. Your task is to get the maximum subsequence below a certain length.
def max_subseq(n, l):
"""
Return the maximum subsequence of length at most l that can be found in the given number n.
For example, for n = 20125 and l = 3, we have that the subsequences are
2
0
1
2
5
20
21
22
25
01
02
05
12
15
25
201
202
205
212
215
225
012
015
025
125
and of these, the maximum number is 225, so our answer is 225.
>>> max_subseq(20125, 3)
225
>>> max_subseq(20125, 5)
20125
>>> max_subseq(20125, 6) # note that 20125 == 020125
20125
>>> max_subseq(12345, 3)
345
>>> max_subseq(12345, 0) # 0 is of length 0
0
>>> max_subseq(12345, 1)
5
"""
"*** YOUR CODE HERE ***"
There are two key insights for this problem:
- You need to split into two cases, the one where the last digit is used and the one where it is not. In the case where it is, we want to reduce
lsince we used the last digit, and in the case where it isn't, we do not. - In the case where we are using the last digit, you need to put the digit back onto the end, and the way to attach a digit
dto the end of a numbernis10 * n + d.