Instructions

In this lab, you have one task: Complete the required problems described in section 3 and submit your code.

The starter code for these problems is provided in lab04.py.

Submission: As instructed before, you need to submit your work with Ok by python ok --submit. You may submit more than once before the deadline, and your score of this assignment will be the highest one of all your submissions.

Readings: You might find the following reference to the textbook useful:

Review

Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the next section and refer back here when you get stuck.

Data Abstraction

Data abstraction is a powerful concept in computer science that allows programmers to treat code as objects -- for example, car objects, chair objects, people objects, etc. That way, programmers don't have to worry about the detail of code/implementation -- we just have to know what it does instead of how it is done.

Data abstraction mimics how we think about the world. When you want to drive a car, you don't need to know how the engine was built or what kind of material the tires are made of. You just have to know how to turn the wheel and press the gas pedal.

In programming languages, an important way to abstraction is to use abstract data types. An abstract data type (ADT for short) consists of two types of functions:

Constructors: functions that create the abstract data using existing information.
Selectors: functions that retrieve information from the abstract data.

Programmers design ADTs to abstract away how information is stored and calculated such that the users of these data types do not need to know how constructors and selectors are implemented. The nature of abstract data types allows users to assume that the functions have been written correctly and work as described, and they just have to use them (without worrying the details).

List

List is a Python data structure that can store multiple elements. Each element can be any type and can even be another list! A list is written as a comma separated list of expressions within a pair of square brackets:


>>> list_of_nums = [1, 2, 3, 4]
>>> list_of_bools = [True, True, False, False]
>>> nested_lists = [1, [2, 3], [4, [5]]]

Each element in a list has an index. Lists are zero-indexed, meaning their indices start at 0 and increase in sequential order. To retrieve an element from a list, we can use list indexing:


>>> lst = [6, 5, 4, 3, 2, 1]
>>> lst[0]
6
>>> lst[3]
3

Often times we need to know how long a list is when we're working with it. To find the length of a list, we can call the function len:


>>> len([])
0
>>> len([2, 4, 6, 8, 10])
5

Tip: Recall that empty lists, [], are falsy values. Therefore, you can use an if statement like the following if you only want to do operations on non-empty lists:
if lst:
 # Do stuff with the elements of list
This is equivalent to:
if len(lst) > 0:
 # Do stuff

You can also create a copy of a portion of the list using list slicing. To slice a list, use the syntax: lst[<start index>:<end index>]. This expression evaluates to a new list containing the elements of lst starting at the element at <start index> (inclusive) up to the element at <end index> (exclusive).


>>> lst = [1, 2, 3, 4, 5]
>>> lst[1:4] # Starting from index 1 (inclusive) to 4 (exclusive)
[2, 3, 4]
>>> lst[:3]  # Start index defaults to 0
[1, 2, 3]
>>> lst[3:]  # End index defaults to len(lst)
[4, 5]
>>> lst[:]   # Creates a copy of the whole list
[1, 2, 3, 4, 5]
>>> lst[4:3] # What happens when start index is greater than end index
[]

List Comprehensions

List comprehension is a compact and powerful way of creating new lists out of sequences. The general syntax for a list comprehension is the following:


[<expression> for <element> in <sequence> if <conditional>]

The syntax is designed to read like English: "Compute the expression for each element in the sequence if the conditional is true for that element."

Let's see an example:


>>> [i**2 for i in [1, 2, 3, 4] if i % 2 == 0]
[4, 16]

Here, for each element i in [1, 2, 3, 4] that satisfies the condition i % 2 == 0, we evaluate the expression i**2 and insert the resulting values into a new list. In other words, this list comprehension will create a new list that contains the square of each of the even elements of the original list.

If we were to write the example above using for and if statements, it would take more lines:


>>> lst = []
>>> for i in [1, 2, 3, 4]:
...     if i % 2 == 0:
...         lst = lst + [i**2]
>>> lst
[4, 16]

Note: The if clause in a list comprehension is optional. For example, we can just write:
>>> [i**2 for i in [1, 2, 3, 4]]
[1, 4, 9, 16]

Tree

A tree is a data structure that represents a hierarchy of information. A file system is a good example of a tree structure. For example, within your NJU-SICP folder, you have folders separating your projects, lab assignments, and homework. The next level is folders that separate different assignments, hw01, lab01, hog, etc., and inside those are the files themselves, including the code directory where the starter files are placed. Below is an incomplete diagram of what your NJU-SICP directory might look like:

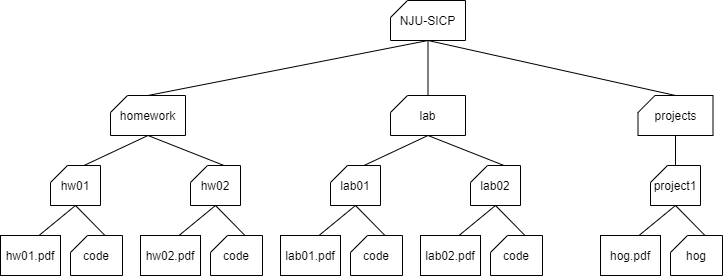
fs-tree

As you can see, unlike trees in the nature, the root of a tree ADT is starting at the top and the leaves are placed at the bottom.

Some terminologies about trees:

root: the node at the top of the tree
label: the value in a node, selected by the label function
branches: a list of trees directly under the tree's root, selected by the branches function
leaf: a tree with zero branches
node: any location within the tree (e.g., root node, leaf nodes, etc.)

Our tree ADT consists of a root and a list of its branches. To create a tree and access its root and branches, we can use the following constructor and selectors:

Constructor
- tree(label, branches=[]): creates a tree object with the given label value at its root node and list of branches. Notice that the second argument to this constructor, branches, is optional - if you want to make a tree with no branches, leave this argument empty.
Selectors
- label(tree): returns the value in the root node of tree.
- branches(tree): returns the list of branches of the given tree.
Convenience function
- is_leaf(tree): returns True if tree's list of branches is empty, and False otherwise.

For example, the tree generated by the following Python code:


number_tree = tree(1, [
                        tree(2),
                        tree(3, [
                                  tree(4),
                                  tree(5)]),
                        tree(6, [
                                  tree(7)])])

would look like this:

Note how we format the code snippet above to make its structure clear, i.e., all nodes from the same level are vertically aligned.

To extract the number 3 from this tree, which is the label of the root of its second branch, we can do this by:


label(branches(number_tree)[1])

The print_tree function prints out a tree in a human-readable form. The exact form follows the pattern illustrated above, where the root is unindented, and each of its branches is indented by one level further.


def print_tree(t, indent=0):
    """Print a representation of this tree in which each node is
    indented by two spaces times its depth from the root.

    >>> print_tree(tree(1))
    1
    >>> print_tree(tree(1, [tree(2)]))
    1
      2
    >>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
    >>> print_tree(numbers)
    1
      2
      3
        4
        5
      6
        7
    """
    print('  ' * indent + str(label(t)))
    for b in branches(t):
        print_tree(b, indent + 1)

Mutability

We say that an object is mutable if its state can be changed as code executes, otherwise we call it immutable. The process of changing an object's state is called mutation. Examples of mutable objects include lists and dictionaries. Examples of objects that are not mutable include tuples and functions.

Note: Remember to distinguish object mutation from variable assignment


>>> l = [1, 2]
>>> l[0] = 114 # Lists are mutable
>>> l
[114, 2]
>>> t = (1, 2)
>>> t[0] = 114 # Tuples are immutable
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'tuple' object does not support item assignment
>>> t = (114, 2) # Variables can be reassigned, though
>>> t[0]
114

We have seen how to use the == operator to check if two expressions evaluate to the same values. We now introduce a new comparison operator, is, that checks if two expressions evaluate to the same identities.

Each object has its own identity. That means you can construct two objects that may look exactly the same but have different identities.


>>> num1 = 257
>>> num2 = 257
>>> num1 == num2
True
>>> num1 is num2
False
>>> lst1 = [1, 2, 3, 4]
>>> lst2 = [1, 2, 3, 4]
>>> lst1 == lst2
True
>>> lst1 is lst2
False

You may find that the behavior of is in some cases is different from what we suggest. For example,
>>> num1 = 10
>>> num2 = 10
>>> num1 is num2
True
This is because python will cache some 'small' objects (i.e., small numbers, short strings, booleans, None, ...). To check more counter examples, see this page

Also note that python will never cache mutable objects.

Here, although the lists referred by lst1 and lst2 have exactly the same contents, they are not the same object. In other words, they are the same in terms of equality, but not in terms of identity (think about twins that look exactly the same but are in fact two different persons).

This is important in the discussion of mutability because when we mutate an object, we simply change its state, not its identity.


>>> lst1 = [1, 2, 3, 4]
>>> lst2 = lst1
>>> lst1.append(5)
>>> lst2
[1, 2, 3, 4, 5]
>>> lst1 is lst2
True

You may think of the name in Python as the pointer variable in the C language, and the identity of an object in Python as the address of an object in the C language. In such an analogy:

assigning an object to a name is similar to assigning the address of this object to a pointer variable,

the == operator compares whether the two pointed values are the same,

and is operator compares whether the two pointers are the same.

You can use the built-in function id to fetch the identity of an object, which differs during different runnings of the Python interpreter. In fact, the expression a is b is equivalent to id(a) == id(b).


>>> lst = [1, 2, 3, 4]
>>> id(lst)
2624875298056 # It may be different on your machine
>>> lst.append(5)
>>> id(lst)
2624875298056

3. What Would Python Display?

In this section, you need to think about what python would display if the code given were input to a python interpreter.

Question1: Lists

Use Ok to test your knowledge with the following "What Would Python Display?" questions:


python ok -q q1 -u

Predict what Python will display when you type the following into the interpreter. Then try it to check your answers.


>>> s = [7//3, 5, [4, 0, 1], 2]
>>> s[0]
______

>>> s[2]
______

>>> s[-1]
______

>>> len(s)
______

>>> 4 in s
______

>>> 4 in s[2]
______

>>> s + [3 + 2, 9]
______

>>> s[2] * 2
______

>>> x = [1, 2, 3, 4]
>>> x[1:3]
______

>>> x[:2]
______

>>> x[1:]
______

>>> x[-2:3]
______

>>> x[-2:4]
______

>>> x[0:4:2]
______

>>> x[::-1]
______

Required Problems

In this section, you are required to complete the problems below and submit your code with Ok as instructed in lab00 to get your answer scored.

4.1 Data Abstractions

Problem 1: Pair Abstraction (150pts)

Define function pair which takes in two elements and returns a function that works as a pair. You will use functions fst and snd to retrieve the values.


def fst(p):
    return p(0)


def snd(p):
    return p(1)


def pair(x, y):
    """Return a function that represents a pair.

    >>> p = pair(1, 2)
    >>> fst(p)
    1
    >>> snd(p)
    2
    """
    "*** YOUR CODE HERE ***"

Since we have defined an abstraction composed of a constructor pair and two selectors fst and snd, now lets use the abstraction to define two functions change_fst and change_snd that modify the pair.

Hint: You should never break the abstraction and ruin the world !


def change_fst(p, v):
    """Change pair p's first element into v and return it.

    >>> p = pair(1, 2)
    >>> fst(p)
    1
    >>> snd(p)
    2
    >>> p = change_fst(p, 3)
    >>> fst(p)
    3
    >>> snd(p)
    2
    """
    "*** YOUR CODE HERE ***"


def change_snd(p, v):
    """Change pair p's second element into v and return it.

    >>> p = pair(1, 2)
    >>> fst(p)
    1
    >>> snd(p)
    2
    >>> p = change_snd(p, 3)
    >>> fst(p)
    1
    >>> snd(p)
    3
    """
    "*** YOUR CODE HERE ***"

Problem 2: City Data Abstraction (200pts)

Say we have an abstract data type for cities. A city has a name, a latitude coordinate, and a longitude coordinate.

Our ADT has one constructor:

make_city(name, lat, lon): Creates a city object with the given name, latitude, and longitude.

We also have the following selectors in order to get the information for each city:

get_name(city): Returns the city's name
get_lat(city): Returns the city's latitude
get_lon(city): Returns the city's longitude

Here is how we would use the constructor and selectors to create cities and extract their information:


    >>> nanjing = make_city('Nanjing', 31, 118)
    >>> get_name(nanjing)
    'Nanjing'
    >>> get_lat(nanjing)
    31
    >>> beijing = make_city('Beijing', 39, 116)
    >>> get_lon(beijing)
    116

All of the selector and constructor functions can be found in the lab file, if you are curious to see how they are implemented. However, the point of data abstraction is that we do not need to know how an abstract data type is implemented, but rather just how we can interact with and use the data type.

Problem 2.1 : Distance (100pts)

We will now implement the function distance, which computes the distance between two city objects. Recall that the distance between two coordinate pairs (x1, y1) and (x2, y2) can be found by calculating the sqrt of (x1 - x2)**2 + (y1 - y2)**2. We have already imported sqrt for your convenience. Use the latitude and longitude of a city as its coordinates; you'll need to use the selectors to access this info!

Hint: Though strange, but in SICP we believe the earth is flat, and we use the euclidean distance.


from math import sqrt

def distance(city1, city2):
    """
    >>> city1 = make_city('city1', 0, 1)
    >>> city2 = make_city('city2', 0, 2)
    >>> distance(city1, city2)
    1.0
    >>> city3 = make_city('city3', 6.5, 12)
    >>> city4 = make_city('city4', 2.5, 15)
    >>> distance(city3, city4)
    5.0
    """
    "*** YOUR CODE HERE ***"

Problem 2.2 : Closer City (100pts)

Next, implement closer_city, a function that takes a latitude, longitude, and two cities, and returns the name of the city that is relatively closer to the provided latitude and longitude.

You may only use the selectors and constructors introduced above and the distance function you just defined for this question.


def closer_city(lat, lon, city1, city2):
    """
    Returns the name of either city1 or city2, whichever is closest to
    coordinate (lat, lon).

    >>> berkeley = make_city('Berkeley', 37.87, 112.26)
    >>> stanford = make_city('Stanford', 34.05, 118.25)
    >>> closer_city(38.33, 121.44, berkeley, stanford)
    'Stanford'
    >>> bucharest = make_city('Bucharest', 44.43, 26.10)
    >>> vienna = make_city('Vienna', 48.20, 16.37)
    >>> closer_city(41.29, 174.78, bucharest, vienna)
    'Bucharest'
    """
    "*** YOUR CODE HERE ***"

4.2 Lists

Problem 3: Deep (50pts)

When nested mutable objects appear, the behavior of your program might be confusing. Consider the example below


>>> inner1 = [1, 2, 3]
>>> inner2 = [4, 5, 6]
>>> a = [inner1, inner2]
>>> a
[[1, 2, 3], [4, 5, 6]]
>>> b1 = a
>>> b2 = a[:]
>>> b3 = [a[0][:], a[1][:]]
>>> b1 == b2 and b2 == b3 and b1 == b3
True
>>> inner1[0] = 222
>>> b1
[[222, 2, 3], [4, 5, 6]]
>>> b2
[[222, 2, 3], [4, 5, 6]]
>>> b3
[[1, 2, 3], [4, 5, 6]]

We call b1 an alias of a, since they are just different names for the same list.
We call b2 a shallow-copy of a, which means b2 is not a, but the contents of b2 are the same objects as the contents of a.
We call b3 a deep-copy of a, as all the contents of b3 (i.e., lists of integers) are created via slicing and are not the same objects as the contents of a.

Now you need to implement a function deep to create a deep-copy of a given non-empty list, whose contents are non-empty lists of integers. In the real-world, objects may be arbitrarily nested (e.g., lists of lists of lists of ...), but in this problem, you only need to handle a simple situation, where the contents of the given list are only lists of integers.

Hint: try to use list comprehension to make your answer concise


def deep(l):
    """Returns a deep-copy of the given list of lists.
    >>> a = [[2, 2, 2], [5, 0, 2], [5, 0, 3]]
    >>> b = deep(a)
    >>> b
    [[2, 2, 2], [5, 0, 2], [5, 0, 3]]
    >>> a is b
    False
    >>> a[0] is b[0]
    False
    >>> a[1] is b[1]
    False
    >>> a[2] is b[2]
    False
    >>> len(a) == len(b)
    True
    """
    "*** YOUR CODE HERE ***"

Problem 4: Reverse (50pts)

my_reverse takes in a list l and returns a new list that contains exactly the same elements in l but in the reverse order.

Hint: use clever slicing.


def my_reverse(l):
    """Returns a new list that contains the exact same elements in l with reversed order.
    >>> a = ['S', 'I', 'C', 'P']
    >>> a is my_reverse(a) # the returned list is newly created
    False
    >>> my_reverse(my_reverse(a)) == a # reverse twice equals to the original list
    True
    >>> my_reverse(a)
    ['P', 'C', 'I', 'S']
    >>> a
    ['S', 'I', 'C', 'P']
    """
    "*** YOUR CODE HERE ***"

Problem 5: Split (50pts)

my_split takes in a list l and a function f and splits the list l into two separate (i.e., a pair of) lists, so that for any element e in the first returned list, f(e) evaluates to True; and for any element e in the second returned list, f(e) evaluates to False.

It is guaranteed that

f is a pure function
f always terminates and
f returns either True or False

Such functions are called predicates, a term from the field of logic.

Hint: use list comprehensions.


def my_split(f, l):
    """Splits the list into a pair of lists according to predicate f.
    >>> my_split(lambda x: True, [1, 2, 3, 4]) # All elements from l conforms to the predicate
    ([1, 2, 3, 4], [])
    >>> my_split(lambda x: x % 2 == 0, [1, 2, 3, 4]) # Split into even and odd numbers
    ([2, 4], [1, 3])
    >>> my_split(lambda x: x < 5, [3, 1, 4, 1, 5, 9, 2])
    ([3, 1, 4, 1, 2], [5, 9])
    >>> my_split(lambda x: not x, [True, False, True, True]) # There might be things other than integers
    ([False], [True, True, True])
    >>> is_ldx = lambda x: not x.startswith('24')
    >>> studentIDs = ['24122', '22122', '502024', '24183']
    >>> ldx, xdx = my_split(is_ldx, studentIDs)
    >>> ldx
    ['22122', '502024']
    >>> studentIDs # You should not mutate the original list
    ['24122', '22122', '502024', '24183']
    """
    "*** YOUR CODE HERE ***"

4.3 Trees

Problem 6: Preorder (100pts)

Define the function preorder, which takes in a tree as an argument and returns a list of all the entries in the tree in the order that print_tree would print them.

The following diagram shows the order that the nodes would get printed, with the arrows representing function calls.

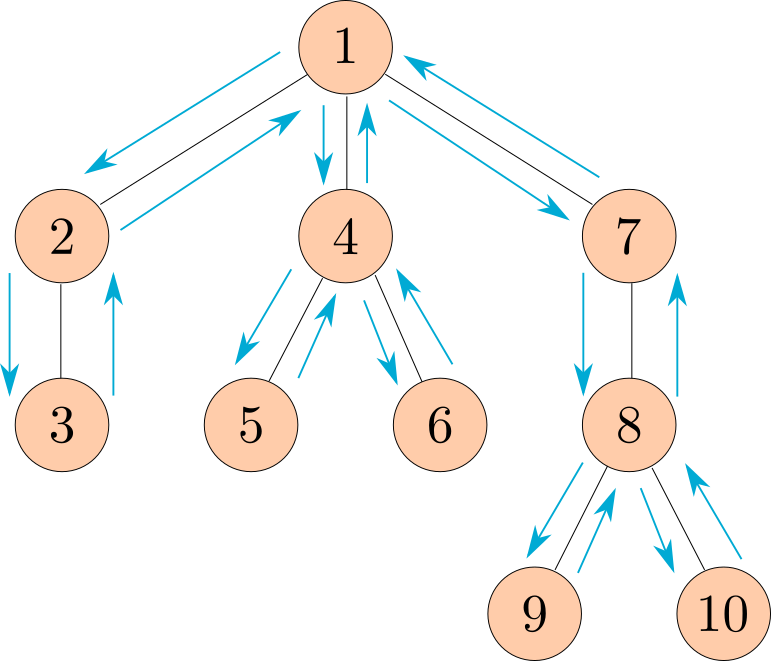
Note: This ordering of the nodes in a tree is called a preorder traversal.


def preorder(t):
    """Return a list of the entries in this tree in the order that they
    would be visited by a preorder traversal (see problem description).

    >>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
    >>> preorder(numbers)
    [1, 2, 3, 4, 5, 6, 7]
    >>> preorder(tree(2, [tree(4, [tree(6)])]))
    [2, 4, 6]
    """
    "*** YOUR CODE HERE ***"

Problem 7 : Nut Finder (100pts)

The squirrels on campus need your help! There are a lot of trees on campus and the squirrels would like to know which ones contain nuts. Define the function nut_finder, which takes in a tree and returns True if the tree contains a node with the value 'nut' and False otherwise.


def nut_finder(t):
    """Returns True if t contains a node with the value 'nut' and
    False otherwise.

    >>> scrat = tree('nut')
    >>> nut_finder(scrat)
    True
    >>> sproul = tree('roots', [tree('branch1', [tree('leaf'), tree('nut')]), tree('branch2')])
    >>> nut_finder(sproul)
    True
    >>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
    >>> nut_finder(numbers)
    False
    >>> t = tree(1, [tree('nut',[tree('not nut')])])
    >>> nut_finder(t)
    True
    """
    "*** YOUR CODE HERE ***"

Problem 8: Sprout leaves (100pts)

Define a function sprout_leaves that takes in a tree, t, and a list of values, values. It produces a new tree that is identical to t, but where each old leaf node has new branches, one for each value in values.

For example, say we have the tree t = tree(1, [tree(2), tree(3, [tree(4)])]):

If we call sprout_leaves(t, [5, 6]), the result is the following tree:


def sprout_leaves(t, values):
    """Sprout new leaves containing the data in values at each leaf in
    the original tree t and return the resulting tree.

    >>> t1 = tree(1, [tree(2), tree(3)])
    >>> print_tree(t1)
    1
      2
      3
    >>> new1 = sprout_leaves(t1, [4, 5])
    >>> print_tree(new1)
    1
      2
        4
        5
      3
        4
        5

    >>> t2 = tree(1, [tree(2, [tree(3)])])
    >>> print_tree(t2)
    1
      2
        3
    >>> new2 = sprout_leaves(t2, [6, 1, 2])
    >>> print_tree(new2)
    1
      2
        3
          6
          1
          2
    """
    "*** YOUR CODE HERE ***"

4.4 Mutability

Problem 9: Insert (100pts)

Write a function insert_items which takes as input a list lst, an argument entry, and another argument elem.

This function will check through each item present in lst to see if it is equivalent with entry. Upon finding an equivalent entry, the function should modify the list by placing elem into the list right after the found entry.

At the ending of the function, the modified list should be returned.

See the doctests for examples about the usage of this function. Use list mutation to modify the original list, no new lists should be created or returned.

Be careful in situations where the values passed into entry and elem are equivalent, so as not to create an infinitely long list while iterating through it. If you find that your code is taking more than a few seconds to run, it is most likely that the function is in a loop of inserting new values.


def insert_items(lst, entry, elem):
    """
    >>> test_lst = [1, 5, 8, 5, 2, 3]
    >>> new_lst = insert_items(test_lst, 5, 7)
    >>> new_lst
    [1, 5, 7, 8, 5, 7, 2, 3]
    >>> large_lst = [1, 4, 8]
    >>> large_lst2 = insert_items(large_lst, 4, 4)
    >>> large_lst2
    [1, 4, 4, 8]
    >>> large_lst3 = insert_items(large_lst2, 4, 6)
    >>> large_lst3
    [1, 4, 6, 4, 6, 8]
    >>> large_lst3 is large_lst
    True
    """
    "*** YOUR CODE HERE ***"

Hint: You may use the lst.insert(ind, obj) to insert an element obj to a position indexed by ind. Search the internet for more information about its usage. Here is just a reference from Python Documentation.

lab04: Data Abstraction