Problem 1: Integration (100pts)

Calculus might be the hardest course you'll meet in college. It is common to calculate definite integral of a continuous function over a closed interval.

Finding the closed form of integrals of polynomial functions such as \( \int_{1}^{2} f(x)=x^2 dx \) might seem simple to you, but the general idea of definite integral calculation is in fact hard (If you are good at this, you must be one of the 积佬s).

A prevalent way of doing definite integration via computers is to approximate the result. To be specific, we divide the given interval \( [l, r] \) into (usually two) smaller intervals \( [l, \frac{l + r}{2}] \) and \( [\frac{l + r}{2}, r] \), and compute the definite integral over these two smaller intervals using recursion.

When the length of the interval \( [l, r] \) is less than the given parameter min_interval, we no longer divide the interval into smaller parts and return immediately the approximation value of the definite integral over \( [l, r] \) using a trapezoidal area.

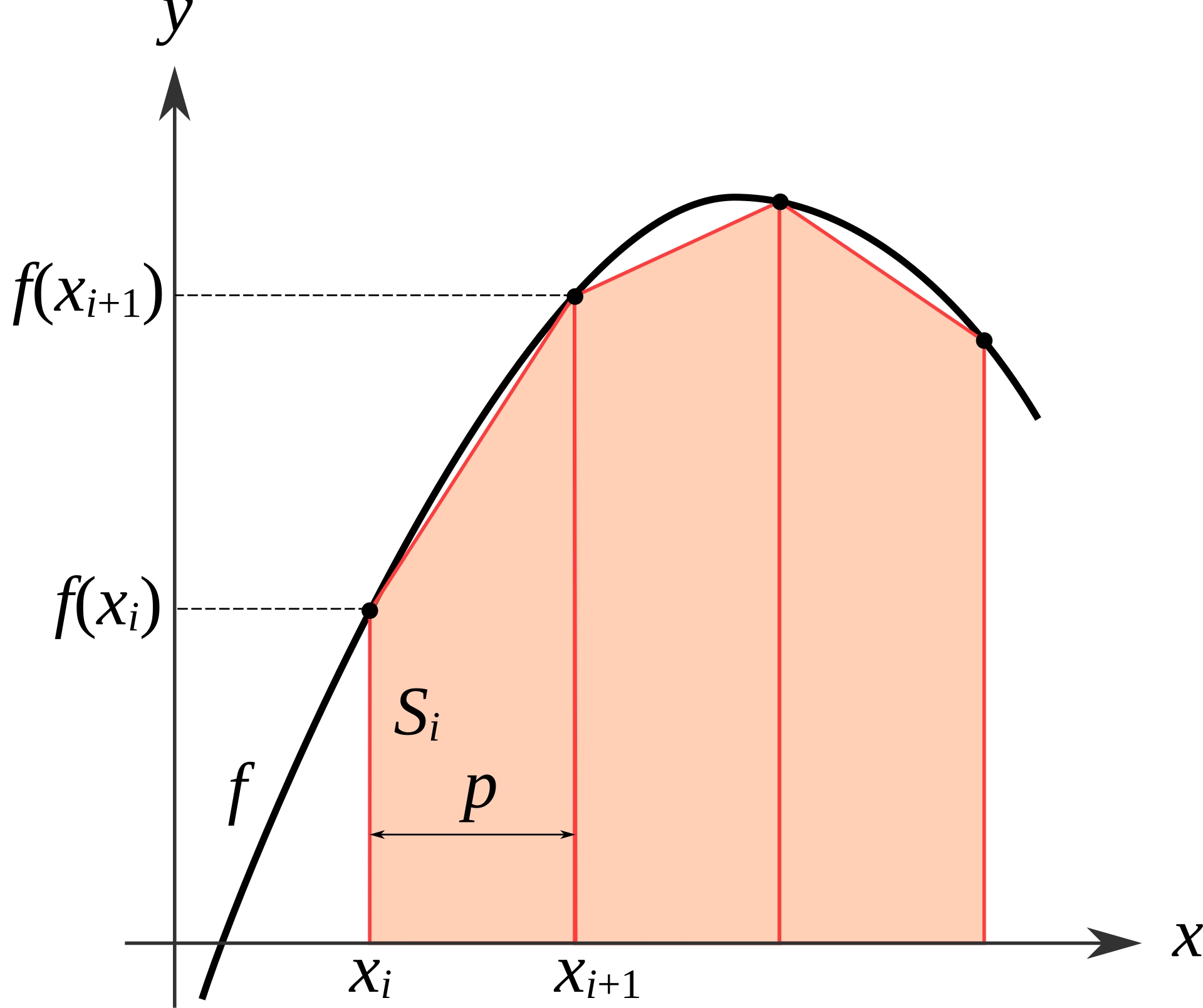
Write a recursive function integrate that takes in a function f, an closed interval l, r, and a interval length limit min_interval. integrate returns the definite integral of function f over interval [l, r], with interval limit min_interval. For example, integrate(lambda x: x * x, 1, 2, 0.01) returns the result of integrating the quadratic function \( f(x)=x^2 \) over interval \( [1, 2] \), with interval length limit \( 0.01 \).

Note: Since we are approximating a calculation, the result need not to be exactly the same as the closed-form. Instead, a relative-error is introduced to judge how precisely your answer approximates the real result. An implementation is considered correct as long as it differs not much from the actual result.

Use recursion - the tests will fail if you use any loop statements.

def integrate(f, l, r, min_interval):
    """Return the definite integration of function f over interval 
    [l,r], with interval length limit min_interval.

    >>> abs(integrate(lambda x: x * x, 1, 2, 0.01) - (7 / 3)) < 0.001
    True
    >>> abs(integrate(lambda x: x, 1, 2, 0.01) - 1.5) < 0.0001
    True
    >>> from construct_check import check
    >>> # ban while or for loops
    >>> check(HW_SOURCE_FILE, 'integrate', ['While', 'For'])
    True
    """
    "*** YOUR CODE HERE ***"