Instructions
In this homework, you are required to complete the problems described in section 2. The starter code for these problems is provided in hw03.py, which is distributed as part of the homework materials in the code directory.
We have also prepared two optional problems just for fun in section 3. You can find further descriptions there.
Submission: As instructed before, you need to submit your work with Ok by python ok --submit.
You may submit more than once before the deadline,
and your score of this assignment will be the highest one of all your submissions.
Readings: You might find the following references to the textbook useful:
The
construct_checkmodule inconstruct_check.pyis used in this assignment, which defines the function check. For example, a call such ascheck("foo.py", "func1", ["While", "For", "Recursion"])checks that the function
func1in filefoo.pydoes not contain any while or for constructs, and is not an overtly recursive function (i.e., one in which a function contains a call to itself by name). Note that this restriction does not apply to all problems in this assignment. If this restriction applies, you will see a call to check somewhere in the problem's doctests.
Required Problems
In this section, you are required to complete the problems below and submit your code to OJ website.
Remember, you can use ok to test your code:
$ python ok # test all functions
$ python ok -q <func> # test single function
Problem 1: Integration (100pts)
Calculus might be the hardest course you'll meet in college. It is common to calculate definite integral of a continuous function over a closed interval.
Finding the closed form of integrals of polynomial functions such as \( \int_{1}^{2} f(x)=x^2 dx \) might seem simple to you, but the general idea of definite integral calculation is in fact hard (If you are good at this, you must be one of the 积佬s).
A prevalent way of doing definite integration via computers is to approximate the result. To be specific, we divide the given interval \( [l, r] \) into (usually two) smaller intervals \( [l, \frac{l + r}{2}] \) and \( [\frac{l + r}{2}, r] \), and compute the definite integral over these two smaller intervals using recursion.
When the length of the interval \( [l, r] \) is less than the given parameter min_interval, we no longer divide the interval into smaller parts and return immediately the approximation value of the definite integral over \( [l, r] \) using a trapezoidal area.
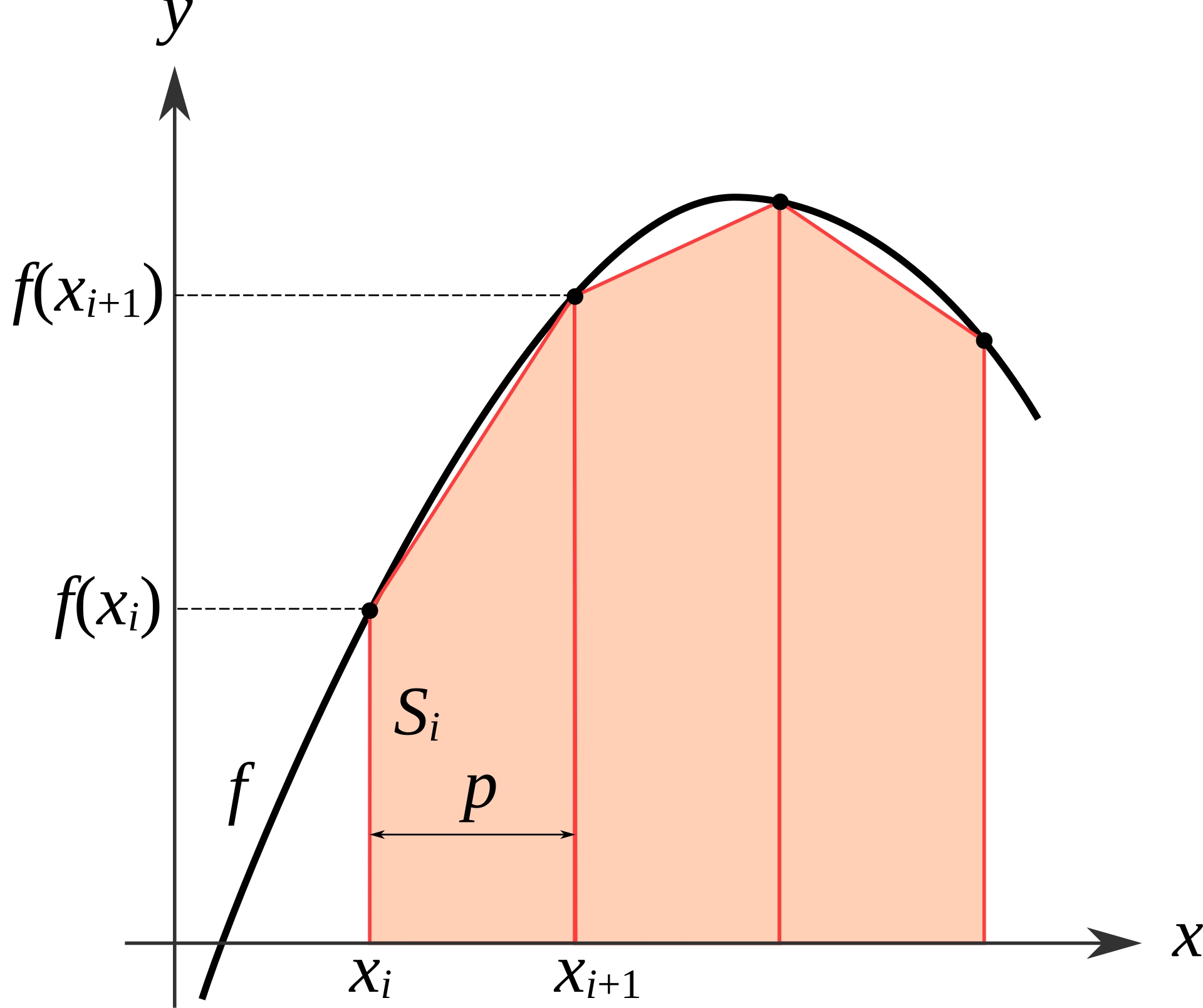
Write a recursive function integrate that takes in a function f, an closed interval l, r, and a interval length limit min_interval.
integrate returns the definite integral of function f over interval [l, r], with interval limit min_interval.
For example, integrate(lambda x: x * x, 1, 2, 0.01) returns the result of integrating the quadratic function \( f(x)=x^2 \) over interval \( [1, 2] \), with interval length limit \( 0.01 \).
Note: Since we are approximating a calculation, the result need not to be exactly the same as the closed-form. Instead, a relative-error is introduced to judge how precisely your answer approximates the real result. An implementation is considered correct as long as it differs not much from the actual result.
Use recursion - the tests will fail if you use any loop statements.
def integrate(f, l, r, min_interval):
"""Return the definite integration of function f over interval
[l,r], with interval length limit min_interval.
>>> abs(integrate(lambda x: x * x, 1, 2, 0.01) - (7 / 3)) < 0.001
True
>>> abs(integrate(lambda x: x, 1, 2, 0.01) - 1.5) < 0.0001
True
>>> from construct_check import check
>>> # ban while or for loops
>>> check(HW_SOURCE_FILE, 'integrate', ['While', 'For'])
True
"""
"*** YOUR CODE HERE ***"
Problem 2: Ping-pong (200pts)
The ping-pong sequence counts up starting from 1 and is always either counting up or counting down. At element k, the direction switches if k is a multiple of 6 or contains the digit 6. The first 30 elements of the ping-pong sequence are listed below, with direction swaps marked using brackets at the 6th, 12th, 16th, 18st, 24th, 26th and 30th elements:
| Index | 1 | 2 | 3 | 4 | 5 | [6] | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| PingPong Value | 1 | 2 | 3 | 4 | 5 | [6] | 5 | 4 | 3 | 2 |
| Index (cont.) | 11 | [12] | 13 | 14 | 15 | [16] | 17 | [18] | 19 | 20 |
| PingPong Value | 1 | [0] | 1 | 2 | 3 | [4] | 3 | [2] | 3 | 4 |
| Index (cont.) | 21 | 22 | 23 | [24] | 25 | [26] | 27 | 28 | 29 | [30] |
| PingPong Value | 5 | 6 | 7 | [8] | 7 | [6] | 7 | 8 | 9 | [10] |
Implement a function pingpong that returns the nth element of the ping-pong sequence without using any assignment statements.
Use recursion - the tests will fail if you use any assignment statements.
Hint1: If you're stuck, first try implementing
pingpongusing assignment statements and awhilestatement. Then, to convert this into a recursive solution, write a helper function that has a parameter for each variable that changes values in the body of the while loop.Hint2: You may need a helper function
contains_sixto check whether the given number contains digit 6.
注意:我们期望你的“递归”代码和等价的“循环”代码有差不多的效率。这道题的
n可能很大,你应该试试你的代码计算pingpong(500)要花多少时间(一瞬间?几秒钟?还是几千年?)才能得到结果。
def pingpong(n):
"""Return the nth element of the ping-pong sequence.
>>> pingpong(7)
5
>>> pingpong(8)
4
>>> pingpong(15)
3
>>> pingpong(21)
5
>>> pingpong(22)
6
>>> pingpong(30)
10
>>> pingpong(68)
0
>>> pingpong(69)
1
>>> pingpong(70)
0
>>> pingpong(71)
-1
>>> pingpong(72)
-2
>>> pingpong(100)
6
>>> from construct_check import check
>>> # ban assignment statements
>>> check(HW_SOURCE_FILE, 'pingpong', ['Assign', 'AugAssign'])
True
"""
"*** YOUR CODE HERE ***"
Problem 3: Balanced Parentheses (100pts)
A parentheses sequence is a string consisting of left parenthesis ( and right parenthesis ).
A parentheses sequence is balanced when every left parenthesis has a corresponding right parenthesis and the pairs of parentheses are properly nested.
For example, () and (())() are balanced parentheses sequences, while ( and ()())) are not.
Formally, a parentheses sequence s is balanced if:
sis empty.sstarts with a(, ends with a), and the rest part ofsis balanced. For example,().scan be divided into two consecutive balanced parentheses sequence. For example,()(())is balanced since it can be divided into()and(()).
Write a recursive function balanced that takes a parentheses sequence s and returns whether s is balanced.
For example, balanced('()') returns True, while balanced(')') and balanced('(') return False.
Hint1: Read the docstring of the three given helper functions
divide,peelandmatch, and try to make the best use of them.Hint2: Don't be afraid to use loops when you have to!
def balanced(s):
"""Returns whether the given parentheses sequence s is balanced.
>>> balanced('()')
True
>>> balanced(')')
False
>>> balanced('(())')
True
>>> balanced('()()')
True
>>> balanced('()())')
False
>>> balanced('()(()')
False
"""
def divide(s, k):
"""Divide the given parentheses sequence s into two parts at position k.
>>> left, right = divide('()()', 2)
>>> left
'()'
>>> right
'()'
>>> left, right = divide('(())()', 4)
>>> left
'(())'
>>> right
'()'
>>> left, right = divide('(())()', 6)
>>> left
'(())()'
>>> right
''
"""
return (s[:k], s[k:])
def peel(s):
"""Peel off the leftmost and rightmost parentheses in s to obtain the
internal part of the parentheses sequence.
>>> peel('(())')
'()'
>>> peel('()')
''
>>> peel('))((')
')('
"""
return s[1:-1]
def match(s):
"""Returns whether the leftmost and the rightmost parentheses in s match.
>>> match('()')
True
>>> match('()()')
True
>>> match('()))')
True
>>> match('))')
False
>>> match(')())')
False
"""
return s[0] == '(' and s[-1] == ')'
"*** YOUR CODE HERE ***"
Problem 4: Count change (200pts)
Denomination is a proper description of a currency amount, usually for coins or banknotes. For example, we have 1 Yuan coins and 100 Yuan bills in Chinese Yuan.
A currency system can be described by a special function that takes in an argument ith and returns the ith smallest denomination in that currency system.
For example, the following money function describes Chinese Yuan (1 Yuan, 5 Yuan, 10 Yuan, 20 Yuan, 50 Yuan and 100 Yuan).
chinese_yuan(2) returns 5 as 5 Yuan is the second smallest denomination.
When ith does not correspond to any denomination, money function returns None.
For example, chinese_yuan(7) yields None since there are only 6 distinct denominations in Chinese Yuan.
def chinese_yuan(ith):
if ith == 1:
return 1
if ith == 2:
return 5
if ith == 3:
return 10
if ith == 4:
return 20
if ith == 5:
return 50
if ith == 6:
return 100
Given an amount of money total and a currency system, a set of banknotes (coins) makes change for total if sum of their values is exactly total. For example, the following sets make change for 15 Chinese Yuan:
- 15*1-Yuan
- 10*1-Yuan + 1*5-Yuan
- 5*1-Yuan + 2*5-Yuan
- 5*1-Yuan + 1*10-Yuan
- 3*5-Yuan
- 1*5-Yuan + 1*10-Yuan
Thus, there are 6 different ways to make change for 15 Chinese Yuan.
Write a recursive function count_change that takes a positive integer total and a money function money and returns the number of ways to make change for total under the currency system described by money.
Hint: Refer to the implementation of
count_partitionsfor an example of how to count the ways to sum up to a total with smaller parts. If you need to keep track of more than one value across recursive calls, consider writing a helper function and pass around the intermediate values as the arguments of the helper function.
def count_change(total, money):
"""Return the number of ways to make change for total,
under the currency system described by money.
>>> def chinese_yuan(ith):
... if ith == 1:
... return 1
... if ith == 2:
... return 5
... if ith == 3:
... return 10
... if ith == 4:
... return 20
... if ith == 5:
... return 50
... if ith == 6:
... return 100
>>> def us_cent(ith):
... if ith == 1:
... return 1
... if ith == 2:
... return 5
... if ith == 3:
... return 10
... if ith == 4:
... return 25
>>> count_change(15, chinese_yuan)
6
>>> count_change(49, chinese_yuan)
44
>>> count_change(49, us_cent)
39
>>> count_change(49, lambda x: 2 ** (x - 1))
692
>>> from construct_check import check
>>> # ban iteration
>>> check(HW_SOURCE_FILE, 'count_change', ['While', 'For'])
True
"""
"*** YOUR CODE HERE ***"
Problem 5: Towers of Hanoi (100pts)
A classic puzzle called the Towers of Hanoi is a game that consists of three rods, and a number of disks of different sizes which can slide onto any rod. The puzzle starts with n disks in a neat stack in ascending order of size on a start rod, the smallest at the top, forming a conical shape.

The objective of the puzzle is to move the entire stack to an end rod, obeying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the top (smallest) disk from one of the rods and sliding it onto another rod, on top of the other disks that may already be present on that rod.
- No disk may be placed on top of a smaller disk.
Complete the definition of move_stack, which prints out the steps required to move n disks from the start rod to the end rod without violating the rules. The provided print_move function will print out the step to move a single disk from the given origin to the given destination.
Hint: Draw out a few games with various
non a piece of paper and try to find a pattern of disk movements that applies to anyn. In your solution, take the recursive leap of faith whenever you need to move any amount of disks less thannfrom one rod to another. If you need more help, see the following hints.
Extra hints
- Hint1: See the animation of the Towers of Hanoi, found on Wikimedia by user Trixx
- Hint2: The strategy used in Towers of Hanoi is to move all but the bottom disc to the second peg, then moving the bottom disc to the third peg, then moving all but the second disc from the second to the third peg.
- Hint3: One thing you don't need to worry about is collecting all the steps.
def print_move(origin, destination):
"""Print instructions to move a disk."""
print("Move the top disk from rod", origin, "to rod", destination)
def move_stack(n, start, end):
"""Print the moves required to move n disks on the start pole to the end
pole without violating the rules of Towers of Hanoi.
n -- number of disks
start -- a pole position, either 1, 2, or 3
end -- a pole position, either 1, 2, or 3
There are exactly three poles, and start and end must be different. Assume
that the start pole has at least n disks of increasing size, and the end
pole is either empty or has a top disk larger than the top n start disks.
>>> move_stack(1, 1, 3)
Move the top disk from rod 1 to rod 3
>>> move_stack(2, 1, 3)
Move the top disk from rod 1 to rod 2
Move the top disk from rod 1 to rod 3
Move the top disk from rod 2 to rod 3
>>> move_stack(3, 1, 3)
Move the top disk from rod 1 to rod 3
Move the top disk from rod 1 to rod 2
Move the top disk from rod 3 to rod 2
Move the top disk from rod 1 to rod 3
Move the top disk from rod 2 to rod 1
Move the top disk from rod 2 to rod 3
Move the top disk from rod 1 to rod 3
"""
assert 1 <= start <= 3 and 1 <= end <= 3 and start != end, "Bad start/end"
"*** YOUR CODE HERE ***"
Problem 6: Multiadder (100pts)
An order 1 numeric function is a function that takes a number and returns a number. An order 2 numeric function is a function that takes a number and returns an order 1 numeric function. Likewise, an order n numeric function is a function that takes a number and returns an order n-1 numeric function. The argument sequence of a nested call expression is the sequence of all arguments in all subexpressions, in the order they appear. For example, the expression f(3)(4)(5)(6)(7) has the argument sequence 3, 4, 5, 6, 7. Note that all numeric functions are pure functions.
Implement multiadder, which takes a positive integer n and returns an order n numeric function that sums an argument sequence of length n.
def multiadder(n):
"""Return a function that takes N arguments, one at a time, and adds them.
>>> f = multiadder(3)
>>> f(5)(6)(7) # 5 + 6 + 7
18
>>> multiadder(1)(5)
5
>>> multiadder(2)(5)(6) # 5 + 6
11
>>> multiadder(4)(5)(6)(7)(8) # 5 + 6 + 7 + 8
26
>>> from construct_check import check
>>> # Make sure multiadder is a pure function.
>>> check(HW_SOURCE_FILE, 'multiadder',
... ['Nonlocal', 'Global'])
True
"""
"*** YOUR CODE HERE ***"
Just for fun Problems
This section is out of scope for our course, so the problems below is optional. That is, the problems in this section don't count for your final score and don't have any deadline. Do it at any time if you want an extra challenge or some practice with higher order function and abstraction!
To check the correctness of your answer, you can submit your code to Contest 'Just for fun'.
Problem 7: Anonymous factorial (0pts)
The recursive factorial function can be written as a single expression by using a conditional expression.
>>> fact = lambda n: 1 if n == 1 else mul(n, fact(sub(n, 1)))
>>> fact(5)
120
The ternary operator
<a> if <bool-exp> else <b>evaluates to<a>if<bool-exp>is truthy and evaluates to<b>if<bool-exp>is false-y.
However, this implementation relies on the fact (no pun intended) that fact has a name, to which we refer in the body of fact. To write a recursive function, we have always given it a name using a def or assignment statement so that we can refer to the function within its own body. In this question, your job is to define fact recursively without giving it a name!
Write an expression that computes n factorial using only call expressions, conditional expressions, and lambda expressions (no assignment or def statements). Note in particular that you are not allowed to use make_anonymous_factorial in your return expression. The sub and mul functions from the operator module are the only built-in functions required to solve this problem:
from operator import sub, mul
def make_anonymous_factorial():
"""Return the value of an expression that computes factorial.
>>> make_anonymous_factorial()(5)
120
>>> from construct_check import check
>>> # ban any assignments or recursion
>>> check(HW_SOURCE_FILE, 'make_anonymous_factorial', ['Assign', 'AugAssign', 'FunctionDef', 'Recursion'])
True
"""
return 'YOUR_EXPRESSION_HERE'
Problem 8: All-Ys Has Been (0pts)
Given mystery function Y, complete fib_maker and number_of_six_maker so that the given doctests work correctly.
When Y is called on fib_maker, it should return a function which takes a positive integer n and returns the nth Fibonacci number.
Similarly, when Y is called on number_of_six_maker it should return a function that takes a positive integer x and returns the number of times the digit 6 appears in x.
Hint: You may use the ternary operator
<a> if <bool-exp> else <b>, which evaluates to<a>if<bool-exp>is truthy and evaluates to<b>if<bool-exp>is false-y.
def Y(f): return (lambda x: x(x))(lambda x: f(lambda z: x(x)(z)))
def fib_maker(f): return lambda r: 'YOUR_EXPRESSION_HERE'
def number_of_six_maker(f): return lambda r: 'YOUR_EXPRESSION_HERE'
my_fib = Y(fib_maker)
my_number_of_six = Y(number_of_six_maker)
# This code sets up doctests for my_fib and my_number_of_six.
my_fib.__name__ = 'my_fib'
my_fib.__doc__ = """Given n, returns the nth Fibonacci nuimber.
>>> my_fib(0)
0
>>> my_fib(1)
1
>>> my_fib(2)
1
>>> my_fib(3)
2
>>> my_fib(4)
3
>>> my_fib(5)
5
"""
my_number_of_six.__name__ = 'my_number_of_six'
my_number_of_six.__doc__ = """Return the number of 6 in each digit of a positive integer n.
>>> my_number_of_six(666)
3
>>> my_number_of_six(123456)
1
"""
Remember to use Ok to test your code:
$ python ok -q my_fib
$ python ok -q my_number_of_six