Problem 3.4: Is BST (200 pts)
Write a function is_bst, which takes a Tree t and returns True if, and only if, t is a valid binary search tree(BST), which means that:
- Each node has at most two children (a leaf is automatically a valid binary search tree)
- The children are valid binary search trees
- For every node
n, the label of every node inn's left child are less than or equal to the label ofn - For every node
n, the label of every node inn's right child are greater than the label ofn
An example of a BST is:
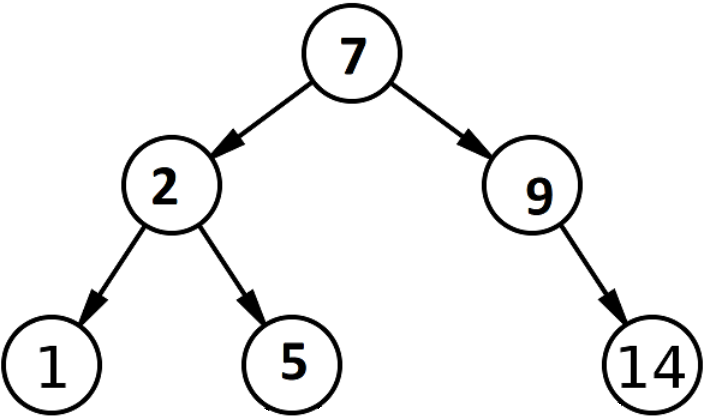
Note: If a node has only one child, that child could be considered either the left or right child. You should take this into consideration.
There is more than one way to solve this problem. Can you come up with more solutions?
def is_bst(t):
"""Returns True if the Tree t has the structure of a valid BST.
>>> t1 = Tree(6, [Tree(2, [Tree(1), Tree(4)]), Tree(7, [Tree(7), Tree(8)])])
>>> is_bst(t1)
True
>>> t2 = Tree(8, [Tree(2, [Tree(9), Tree(1)]), Tree(3, [Tree(6)]), Tree(5)])
>>> is_bst(t2)
False
>>> t3 = Tree(6, [Tree(2, [Tree(4), Tree(1)]), Tree(7, [Tree(7), Tree(8)])])
>>> is_bst(t3)
False
>>> t4 = Tree(1, [Tree(2, [Tree(3, [Tree(4)])])])
>>> is_bst(t4)
True
>>> t5 = Tree(1, [Tree(0, [Tree(-1, [Tree(-2)])])])
>>> is_bst(t5)
True
>>> t6 = Tree(1, [Tree(4, [Tree(2, [Tree(3)])])])
>>> is_bst(t6)
True
>>> t7 = Tree(2, [Tree(1, [Tree(5)]), Tree(4)])
>>> is_bst(t7)
False
"""
"*** YOUR CODE HERE ***"
Hint: It may be helpful to write helper functions
bst_minandbst_maxthat return the minimum and maximum, respectively, of a Tree if it is a valid binary search tree.