1. Instructions

In this homework, you are required to complete the problems described in section 2. The starter code for these problems is provided in hw07.py, which is distributed as part of the homework materials in the code directory.

We have also prepared some optional problems just for fun in section 4. You can find further descriptions there.

Submission: As instructed before, you need to submit your work with Ok by python ok --submit. You may submit more than once before the deadline, and your score of this assignment will be the highest one of all your submissions.

Readings: You might find the following references to the textbook useful:

2. Required Problems

In this section, you are required to complete the problems below and submit your code to OJ website.

Remember, you can use ok to test your code:

$ python ok  # test all functions
$ python ok -q <class / func>  # test single class / function

Problem 1: Polynomial (100pts)

In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. An example of a polynomial of a single indeterminate \(x\) is \(x^2 − 4x + 7\).

We can use class Polynomial to represent polynomials, and a list of number to represent coefficients. For example, Polynomial([a_0, a_1, ..., a_n]) represents polynomial \(a_0 + a_1x + ... + a_nx^n\).

Implement required methods of class Polynomial such that representing a Polynomial object Polynomial([a_0, a_1, ..., a_n]) displays Polynomial([a_0, a_1, ..., a_n]), printing it displays a_0 + a_1*x^1 + ... + a_n*x^n and we can directly add or multiply two polynomial objects.

Note: the highest degree coefficient of a polynomial should not be 0, unless it is just \(0\).

class Polynomial:
    """Polynomial.

    >>> a = Polynomial([0, 1, 2, 3, 4, 5, 0])
    >>> a
    Polynomial([0, 1, 2, 3, 4, 5])
    >>> print(a)
    0 + 1*x^1 + 2*x^2 + 3*x^3 + 4*x^4 + 5*x^5
    >>> b = Polynomial([-1, 0, -2, 1, -3])
    >>> print(b)
    -1 + 0*x^1 + -2*x^2 + 1*x^3 + -3*x^4
    >>> print(a + b)
    -1 + 1*x^1 + 0*x^2 + 4*x^3 + 1*x^4 + 5*x^5
    >>> print(a * b)
    0 + -1*x^1 + -2*x^2 + -5*x^3 + -7*x^4 + -12*x^5 + -11*x^6 + -15*x^7 + -7*x^8 + -15*x^9
    >>> print(a)
    0 + 1*x^1 + 2*x^2 + 3*x^3 + 4*x^4 + 5*x^5
    >>> print(b) # a and b should not be changed
    -1 + 0*x^1 + -2*x^2 + 1*x^3 + -3*x^4
    >>> zero = Polynomial([0])
    >>> zero
    Polynomial([0])
    >>> print(zero)
    0
    """
    "*** YOUR CODE HERE ***"

Hint1: You can convert numbers to strings using the str function, and you can combine strings together using +.

Hint2: You may find python built-in function enumerate helpful.

Problem 2: Linked List (200pts in total)

The Link class is defined as below.

class Link:
    """A linked list.

    >>> s = Link(1)
    >>> s.first
    1
    >>> s.rest is Link.empty
    True
    >>> s = Link(2, Link(3, Link(4)))
    >>> s.first = 5
    >>> s.rest.first = 6
    >>> s.rest.rest = Link.empty
    >>> s                                    # Displays the contents of repr(s)
    Link(5, Link(6))
    >>> s.rest = Link(7, Link(Link(8, Link(9))))
    >>> s
    Link(5, Link(7, Link(Link(8, Link(9)))))
    >>> print(s)                             # Prints str(s)
    <5 7 <8 9>>
    """
    empty = ()

    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest

    def __repr__(self):
        if self.rest is not Link.empty:
            rest_repr = ', ' + repr(self.rest)
        else:
            rest_repr = ''
        return 'Link(' + repr(self.first) + rest_repr + ')'

    def __str__(self):
        string = '<'
        while self.rest is not Link.empty:
            string += str(self.first) + ' '
            self = self.rest
        return string + str(self.first) + '>'

Problem 2.1: Remove Duplicates (100 pts)

Write a function remove_duplicates which takes in a sorted linked list of integers and mutates it so that all duplicates are removed.

Your implementation should mutate the original linked list. DO NOT create any new linked lists and DO NOT return the modified Link object.

def remove_duplicates(lnk):
    """ Remove all duplicates in a sorted linked list.

    >>> lnk = Link(1, Link(1, Link(1, Link(1, Link(5)))))
    >>> Link.__init__, hold = lambda *args: print("Do not steal chicken!"), Link.__init__
    >>> try:
    ...     remove_duplicates(lnk)
    ... finally:
    ...     Link.__init__ = hold
    >>> lnk
    Link(1, Link(5))
    """
    "*** YOUR CODE HERE ***"

Problem 2.2: Reverse (100 pts)

Write a function reverse which takes in a linked list lnk, reverses the order of it and returns the reversed list(i.e. return a new reference to the head of the reversed list). Your implementation should mutate the original linked list. DO NOT create any new linked lists.

You may not just simply exchange the first to reverse the list. On the contrary, you should make change on rest.

There is more than one way to solve this problem. Can you come up with more solutions?

def reverse(lnk):
    """ Reverse a linked list.

    >>> a = Link(1, Link(2, Link(3)))
    >>> # Disallow the use of making new Links before calling reverse
    >>> Link.__init__, hold = lambda *args: print("Do not steal chicken!"), Link.__init__
    >>> try:
    ...     r = reverse(a)
    ... finally:
    ...     Link.__init__ = hold
    >>> print(r)
    <3 2 1>
    >>> a.first # Make sure you do not change first
    1
    """
    "*** YOUR CODE HERE ***"

Problem 3: Tree (500pts in total)

The Tree class is defined as below.

class Tree:
    """
    >>> t = Tree(3, [Tree(2, [Tree(5)]), Tree(4)])
    >>> t.label
    3
    >>> t.branches[0].label
    2
    >>> t.branches[1].is_leaf()
    True
    """

    def __init__(self, label, branches=[]):
        for b in branches:
            assert isinstance(b, Tree)
        self.label = label
        self.branches = list(branches)

    def is_leaf(self):
        return not self.branches

    def __repr__(self):
        if self.branches:
            branch_str = ', ' + repr(self.branches)
        else:
            branch_str = ''
        return 'Tree({0}{1})'.format(self.label, branch_str)

    def __str__(self):
        def print_tree(t, indent=0):
            tree_str = '  ' * indent + str(t.label) + "\n"
            for b in t.branches:
                tree_str += print_tree(b, indent + 1)
            return tree_str

        return print_tree(self).rstrip()

Problem 3.1: Equal Trees (100 pts)

Recall that when Python evaluates the expression a + b, it is in fact evaluating a.__add__(b). Similarly, when Python evaluates the expression a == b, it is in fact evaluating a.__eq__(b).

Implement special method __eq__ in class Tree, such that we can simply use t1 == t2 to judge whether two trees t1 and t2 are equivalent trees (i.e. have equivalent labels and equivalent branches, and all of their branches are in the same order.).

class Tree:
    ...

    def __eq__(self): # Does this line need to be changed?
        """Returns whether two trees are equivalent.

        >>> t1 = Tree(1, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)]), Tree(7)])
        >>> t1 == t1
        True
        >>> t2 = Tree(1, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)]), Tree(7)])
        >>> t1 == t2
        True
        >>> t3 = Tree(0, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)]), Tree(7)])
        >>> t4 = Tree(1, [Tree(5, [Tree(6)]), Tree(2, [Tree(3), Tree(4)]), Tree(7)])
        >>> t5 = Tree(1, [Tree(2, [Tree(3), Tree(4)]), Tree(5, [Tree(6)])])
        >>> t1 == t3 or t1 == t4 or t1 == t5
        False
        """
        "*** YOUR CODE HERE ***"

Problem 3.2: Generate Paths (100 pts)

Define a generator function generate_paths which takes in a Tree t, a value value, and returns a generator object which yields each path from the root of t to a node that has label value.

t is implemented with a class, not as the function-based ADT.

Each path should be represented as a list of the labels along that path in the tree. You may yield the paths in any order.

def generate_paths(t, value):
    """Yields all possible paths from the root of t to a node with the label value
    as a list.

    >>> t1 = Tree(1, [Tree(2, [Tree(3), Tree(4, [Tree(6)]), Tree(5)]), Tree(5)])
    >>> print(t1)
    1
      2
        3
        4
          6
        5
      5
    >>> next(generate_paths(t1, 6))
    [1, 2, 4, 6]
    >>> path_to_5 = generate_paths(t1, 5)
    >>> sorted(list(path_to_5))
    [[1, 2, 5], [1, 5]]

    >>> t2 = Tree(0, [Tree(2, [t1])])
    >>> print(t2)
    0
      2
        1
          2
            3
            4
              6
            5
          5
    >>> path_to_2 = generate_paths(t2, 2)
    >>> sorted(list(path_to_2))
    [[0, 2], [0, 2, 1, 2]]
    """
    "*** YOUR CODE HERE ***"

Problem 3.3: Count Coins Tree (100 pts)

Nolan wants to help his friends learn tree recursion! They don't really understand all the recursive calls and how they work, so Nolan decides to generate a tree to show the recursive calls in a tree recursion. As a demonstration, he picks the count_coins problem, which is a simplified version of count_change problem in hw03. The following code is his implementation of count_coins problem.

def count_coins(total, denominations):
    """
    Given a positive integer `total`, and a list of denominations,
    a group of coins make change for `total` if the sum of them is `total` 
    and each coin is an element in `denominations`.
    The function `count_coins` returns the number of such groups. 
    """
    if total == 0:
        return 1
    if total < 0:
        return 0
    if len(denominations) == 0:
        return 0
    without_current = count_coins(total, denominations[1:])
    with_current = count_coins(total - denominations[0], denominations)
    return without_current + with_current

Implement count_coins_tree, which takes in a non-negative integer total and a list denominations, and returns a tree representing the recursive calls of count_coins.

Since the recursive tree is usually huge, Nolan decides to include only the recursive calls that eventually lead to a valid way of making change.

The leaves of tree count_coins_tree(15, [1, 5, 10, 25]) are listed below:

15 1-cent coins
10 1-cent, 1 5-cent coins
5 1-cent, 2 5-cent coins
5 1-cent, 1 10-cent coins
3 5-cent coins
1 5-cent, 1 10-cent coin

Note: The label of the tree should be a string.

def count_coins_tree(total, denominations):
    """
    >>> count_coins_tree(1, []) # Return None since there is no way to make change with empty denominations
    >>> t = count_coins_tree(3, [1, 2]) 
    >>> print(t) # 2 ways to make change for 3 cents
    3, [1, 2]
      2, [1, 2]
        2, [2]
          1
        1, [1, 2]
          1
    >>> # 6 ways to make change for 15 cents
    >>> t = count_coins_tree(15, [1, 5, 10, 25]) 
    >>> print(t)
    15, [1, 5, 10, 25]
      15, [5, 10, 25]
        10, [5, 10, 25]
          10, [10, 25]
            1
          5, [5, 10, 25]
            1
      14, [1, 5, 10, 25]
        13, [1, 5, 10, 25]
          12, [1, 5, 10, 25]
            11, [1, 5, 10, 25]
              10, [1, 5, 10, 25]
                10, [5, 10, 25]
                  10, [10, 25]
                    1
                  5, [5, 10, 25]
                    1
                9, [1, 5, 10, 25]
                  8, [1, 5, 10, 25]
                    7, [1, 5, 10, 25]
                      6, [1, 5, 10, 25]
                        5, [1, 5, 10, 25]
                          5, [5, 10, 25]
                            1
                          4, [1, 5, 10, 25]
                            3, [1, 5, 10, 25]
                              2, [1, 5, 10, 25]
                                1, [1, 5, 10, 25]
                                  1
    """
    "*** YOUR CODE HERE ***"

Hint1: The implementation of count_coins_tree will follow a similar logic to count_coins defined above.

Hint2: Return None if it's no way to make change, but do not include None in the tree.

Problem 3.4: Is BST (200 pts)

Write a function is_bst, which takes a Tree t and returns True if, and only if, t is a valid binary search tree(BST), which means that:

Each node has at most two children (a leaf is automatically a valid binary search tree)
The children are valid binary search trees
For every node n, the label of every node in n's left child are less than or equal to the label of n
For every node n, the label of every node in n's right child are greater than the label of n

An example of a BST is:
2_3_4

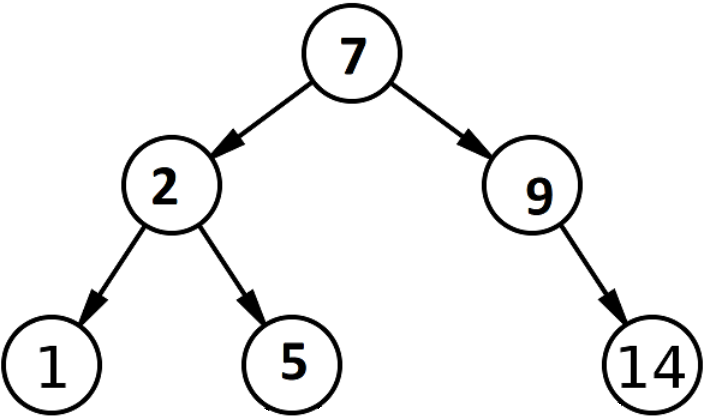
Note: If a node has only one child, that child could be considered either the left or right child. You should take this into consideration.

There is more than one way to solve this problem. Can you come up with more solutions?

def is_bst(t):
    """Returns True if the Tree t has the structure of a valid BST.

    >>> t1 = Tree(6, [Tree(2, [Tree(1), Tree(4)]), Tree(7, [Tree(7), Tree(8)])])
    >>> is_bst(t1)
    True
    >>> t2 = Tree(8, [Tree(2, [Tree(9), Tree(1)]), Tree(3, [Tree(6)]), Tree(5)])
    >>> is_bst(t2)
    False
    >>> t3 = Tree(6, [Tree(2, [Tree(4), Tree(1)]), Tree(7, [Tree(7), Tree(8)])])
    >>> is_bst(t3)
    False
    >>> t4 = Tree(1, [Tree(2, [Tree(3, [Tree(4)])])])
    >>> is_bst(t4)
    True
    >>> t5 = Tree(1, [Tree(0, [Tree(-1, [Tree(-2)])])])
    >>> is_bst(t5)
    True
    >>> t6 = Tree(1, [Tree(4, [Tree(2, [Tree(3)])])])
    >>> is_bst(t6)
    True
    >>> t7 = Tree(2, [Tree(1, [Tree(5)]), Tree(4)])
    >>> is_bst(t7)
    False
    """
    "*** YOUR CODE HERE ***"

Hint: It may be helpful to write helper functions bst_min and bst_max that return the minimum and maximum, respectively, of a Tree if it is a valid binary search tree.

3. Mock Exam Problems

In this section, you can take a mock exam to check your understanding about special method and linked list

Download the mock exam here and print it out.

说明：

你应该先完成本周的作业，有空余时间再来做mock exam。

题目是2021、2020年期末考试（A卷）第一题。建议你打印出来独立完成。

4. Just for fun Problems

This section is out of scope for our course, so the problems below is optional. That is, the problems in this section don't count for your final score and don't have any deadline. Do it at any time if you want an extra challenge or some practice with higher order function and abstraction!

To check the correctness of your answer, you can submit your code to Contest 'Just for fun'.

Problem 4: Has Cycle (0pts)

The Link class can represent lists with cycles. That is, a list may contain itself as a sublist. Implement has_cycle that returns whether its argument lnk, a Link instance, contains a cycle. Try to solve it with constant space! (i.e. no list, dict, set or any other container)

def has_cycle(lnk):
    """ Returns whether `lnk` has cycle.

    >>> lnk = Link(1, Link(2, Link(3)))
    >>> has_cycle(lnk)
    False
    >>> lnk.rest.rest.rest = lnk
    >>> has_cycle(lnk)
    True
    >>> lnk.rest.rest.rest = lnk.rest
    >>> has_cycle(lnk)
    True
    """
    "*** YOUR CODE HERE ***"

Problem 5: Decorate Christmas Tree (0 pts)

Christmas is coming soon. Isla bought a Christmas tree for Tsukasa. A Christmas tree is a Tree instance. There are some gifts on every nodes of the tree, and the label of each node is the number of gifts on it. Every gifts have the same weight.

We say a tree is balanced if it is a leaf or the total weight of its every branches are the same and all its branches are balanced. For example, the left tree is balanced but the right one is not.

3_2

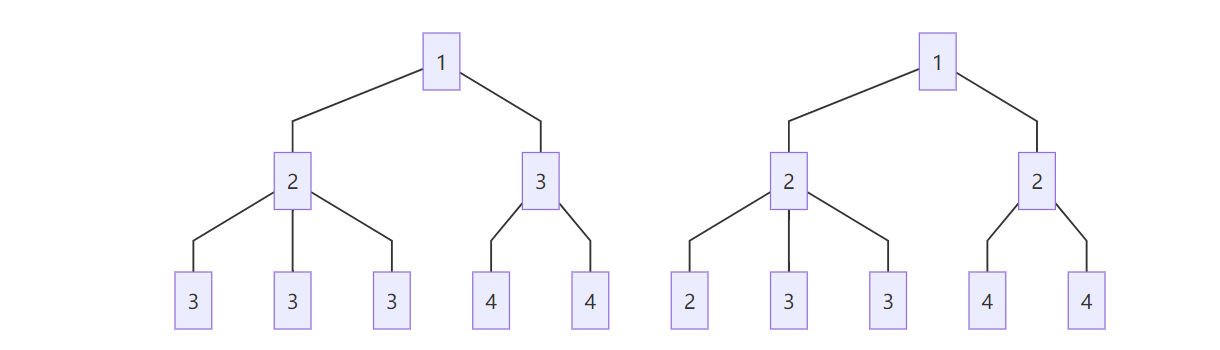
Isla wants to buy more gifts and hang them on the tree to balance it. Please help her implement balance_tree, which takes in a tree t and hangs gifts as few as possible on it to balance it.

Note: For trees which have more than one ways to balance with the same minimum number of gifts, you can choose any one of them as result and it won't influence your score.

def balance_tree(t):
    """Balance a tree.

    >>> t1 = Tree(1, [Tree(2, [Tree(2), Tree(3), Tree(3)]), Tree(2, [Tree(4), Tree(4)])])
    >>> balance_tree(t1)
    >>> t1
    Tree(1, [Tree(2, [Tree(3), Tree(3), Tree(3)]), Tree(3, [Tree(4), Tree(4)])])
    """
    "*** YOUR CODE HERE ***"

Problem 6: Decorate Christmas Tree II (0 pts)

This time, Isla bought 3 super big Christmas trees, which all have more than 30000 nodes! Can you still work out in less than 5 seconds?

Hint1: You should scan every node only constant times.

Hint2: You can set up new attribute of Tree instance in your solution to memorize something! It doesn't violate abstraction barrier.

Homework 07: Special Method, Linked List and Tree